绘制几何形状¶
三大类形状绘制函数¶
在Easy Graphics中,绘制形状的函数可以分为三大类:
- 只绘制形状轮廓线的函数。这类函数用’xxx()’ 的形式命名(“xxx”是所绘制形状的名称,如circle)。下面的程序绘制了一个边线为蓝色的圆。
from easygraphics import *
def main():
init_graph(200, 150)
set_color(Color.BLUE)
set_fill_color(Color.RED)
circle(100, 75, 60)
pause()
close_graph()
easy_run(main)
- 同时绘制形状轮廓并填充形状内部的函数。这类函数用’draw_xxx()’ 的形式命名(“xxx”是所绘制形状的名称,如draw_circle)。下面的程序绘制了一个边线为蓝色内部为红色的圆。
from easygraphics import *
def main():
init_graph(200, 150)
set_color(Color.BLUE)
set_fill_color(Color.RED)
draw_circle(100, 75, 60)
pause()
close_graph()
easy_run(main)
- 不绘制形状轮廓线,只填充形状内部的函数。这类函数用’fill_xxx()’ 形式命名(“xxx”是所绘制形状的名称,如fill_circle)。下面的程序绘制(填充)了一个无边线内部为红色的圆。
from easygraphics import *
def main():
init_graph(200, 150)
set_color(Color.BLUE)
set_fill_color(Color.RED)
fill_circle(100, 75, 60)
pause()
close_graph()
easy_run(main)
 |
 |
 |
| circle() | draw_circle() | fill_circle() |
角¶
在Easygraphics中,所有的角都使用“角度”作为单位。
在画弧(arc),饼(pie)和弓形(chord)时,正的角度值为逆时针旋转;负的角度值为顺时针旋转。0度位于三点钟方向(X轴正向)。
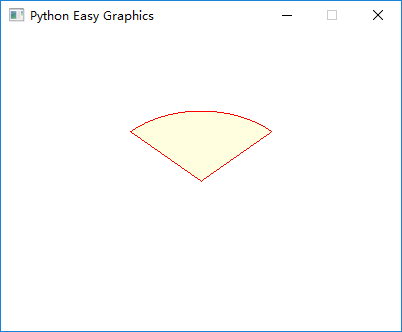
下面的程序画了一个从45度到135度的饼(pie)。
from easygraphics import *
def main():
init_graph(400, 300)
set_color("red")
set_fill_color("lightyellow")
draw_pie(200, 150, 45, 135, 100, 70)
pause()
close_graph()
easy_run(main)
多边形(Polygon)¶
使用polygon()/draw_polygon()/fill_polygon()函数,我们可以绘制或者填充多边形(polygon)。
在绘制多边形时,我们必须指明多边形的各个顶点(vertices)
polygon()/draw_polygon()/fill_polygon()需要提供一个list(列表)参数,其中存放着各顶点的位置。在列表中,每个顶点用两个数来表示(其x和y坐标)。所以,如果有n个顶点,那么列表中应该有2n个数。
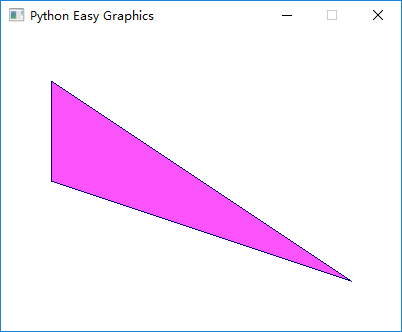
下面的程序绘制了一个三角形,它的三个顶点分别位于 (50, 50), (350,250)和(50, 150):
from easygraphics import *
def main():
init_graph(400, 300)
set_color(Color.DARK_BLUE)
set_fill_color(Color.LIGHT_MAGENTA)
draw_polygon(50, 50, 350, 250, 50, 150)
pause()
close_graph()
easy_run(main)
折线(Polylines)¶
使用poly_line()或draw_poly_line(),我们可以绘制折线。
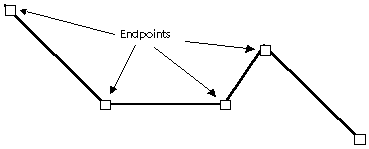
折线(Polyline) 是一条由一个或多个依次相连的线段组成的线。因此,要绘制一条折线,我们必须指明连接各线段的端点
poly_line() and draw_poly_line()需要提供一个list(列表)参数,其中存放着各端点的位置。在列表中,每个端点用两个数来表示(其x和y坐标)。所以n个端点就需要2n个数来表示。
下面程序绘制了一条依次连接了点(50,50)、(350,75)、(50,150)、(350,175)、(50,250)和(350,275)的折线。
from easygraphics import *
def main():
init_graph(400, 300)
draw_poly_line(50, 50, 350, 75, 50, 150, 350, 175, 50, 250, 350, 275)
pause()
close_graph()
easy_run(main)

贝塞尔曲线(Bézier curve)¶
每条贝塞尔曲线由一组控制点P0到Pn定义,其中n是曲线的阶数(n=1称为线性曲线,2为二次曲线,3为三次曲线,以此类推)。第一个和最后一个控制点是曲线的端点,中间的控制点一般则不在曲线上。
三次贝塞尔曲线(Cubic Bézier curves)是最常见的贝塞尔曲线。

平面或者空间中的4个点P0、P1、P2和P3定义了一条贝塞尔曲线。这条曲线从P0出发,走向P1,并从P2的方向到达P3。通常该曲线不会通过P1和P2,这两个点只是为曲线提供方向信息。P1和P2之间的距离决定了曲线在转向P2前,向P1方向前进”多远”和”多快”。
曲线的参数形式为:
我们可以使用bezier()或draw_bezier()来绘制三次贝塞尔曲线。它们需要一个列表作为参数来指明各控制点的位置。在列表中,每个控制点对应两个数值(x和y坐标)。因为一条贝塞尔曲线需要4个控制点,因此列表中应该有8个数。
下面的程序绘制了一条三次贝塞尔曲线,其四个控制点分别为(300,50)、(200,50)、(200,200)和(100,200)。
from easygraphics import *
def main():
init_graph(600, 400)
points = [300, 50, 200, 50, 200, 200, 100, 200]
draw_bezier(*points)
pause()
close_graph()
easy_run(main)
我们可以使用quadratic()或draw_quadratic()来绘制二次贝塞尔曲线。它们需要一个列表作为参数来指明各控制点的位置。在列表中,每个控制点对应两个数值(x和y坐标)。因为一条贝塞尔曲线需要3个控制点,因此列表中应该有6个数。
下面的程序绘制了一条二次贝塞尔曲线,其三个控制点分别为(300,50)、(200,50)和(100,200)。
from easygraphics import *
def main():
init_graph(600, 400)
points = [300, 50, 200, 50, 100, 200]
draw_quadratic(*points)
pause()
close_graph()
easy_run(main)
泛洪填充(Flood Fill)¶
不规则图形可以使用泛洪(flood fill)方式填充。被填充形状的外轮廓线必须完全闭合。下面的程序使用泛洪填充一个花瓣。
from easygraphics import *
def main():
init_graph(400, 200)
arc(200, -40, 180, 360, 220, 220)
arc(200, 240, 0, 180, 220, 220)
set_fill_color(Color.DARK_RED)
flood_fill(200, 100, Color.BLACK)
pause()
close_graph()
easy_run(main)
下面是绘制的结果:

填充规则(Fill Rule)¶
填充规则决定如何填充非凸形状(non-convex shapes)。
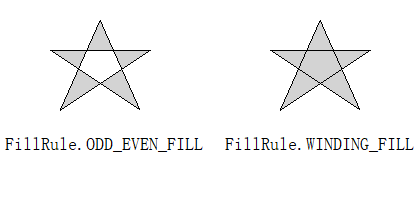
可以使用set_fill_rule()函数来设置填充规则。
缺省的填充规则是奇偶填充(odd even fill)。
from easygraphics import *
def main():
init_graph(420, 200)
set_fill_rule(FillRule.ODD_EVEN_FILL)
set_fill_color("lightgray")
draw_polygon(50, 50, 150, 50, 60, 110, 100, 20, 140,110,50,50)
draw_text(5,150,"FillRule.ODD_EVEN_FILL")
translate(220,0)
set_fill_rule(FillRule.WINDING_FILL)
set_fill_color("lightgray")
draw_polygon(50, 50, 150, 50, 60, 110, 100, 20, 140,110,50,50)
draw_text(5,150,"FillRule.WINDING_FILL")
pause()
close_graph()
easy_run(main)